Jump to content

Newtonian telescope

From Wikipedia, the free encyclopedia
"Newton telescope" redirects here. For the observatory at the Canary Islands, see Isaac Newton Telescope.

Woman looking through a Newtonian telescope

The Newtonian telescope, also called the Newtonian reflector or just a Newtonian, is a type of reflecting telescope invented by the English scientist Sir Isaac Newton, using a concave primary mirror and a flat diagonal secondary mirror. Newton's first reflecting telescope was completed in 1668 and is the earliest known functional reflecting telescope.[1] The Newtonian telescope's simple design has made it very popular with amateur telescope makers.[2]

Description

[edit]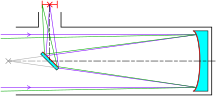
Newtonian telescope design

A Newtonian telescope is composed of a primary mirror or objective, usually parabolic in shape, and a smaller flat secondary mirror. The primary mirror makes it possible to collect light from the pointed region of the sky, while the secondary mirror redirects the light out of the optical axis at a right angle so it can be viewed with an eyepiece.

Advantages of the Newtonian design

[edit]
  • They are free of chromatic aberration found in refracting telescopes.
  • Newtonian telescopes are usually less expensive for any given objective diameter (or aperture) than comparable quality telescopes of other types.
  • Since there is only one surface that needs to be ground and polished into a complex shape, overall fabrication is much simpler than other telescope designs (Gregorians, cassegrains, and early refractors had two surfaces that need figuring. Later achromatic refractor objectives had four surfaces that have to be figured).
  • A short focal ratio can be more easily obtained, leading to a wider field of view.
  • The eyepiece is located at the top end of the telescope. Combined with short f-ratios this can allow for a much more compact mounting system, reducing cost and adding to portability.

Disadvantages of the Newtonian design

[edit]
A large Newtonian with ladder to reach the eyepiece
  • Newtonians, like other reflecting telescope designs using parabolic mirrors, suffer from coma, an off-axis aberration which causes imagery to flare inward and towards the optical axis (stars towards edge of the field of view take on a comet-like shape). This flare is zero on-axis, and is linear with increasing field angle and inversely proportional to the square of the mirror focal ratio (the mirror focal length divided by the mirror diameter). The formula for third order tangential coma is 3θ / 16F², where θ is the angle off axis to the image in radians and F is the focal ratio. Newtonians with a focal ratio of f/6 or lower (f/5 for example) are considered to have increasingly serious coma for visual or photographic use.[3] Low focal ratio primary mirrors can be combined with lenses that correct for coma to increase image sharpness over the field.[4]
  • Newtonians have a central obstruction due to the secondary mirror in the light path. This obstruction and also the diffraction spikes caused by the support structure (called the "spider") of the secondary mirror reduce contrast. Visually, these effects can be reduced by using a two or three-legged curved spider. This reduces the diffraction sidelobe intensities by a factor of about four and helps to improve image contrast, with the potential penalty that circular spiders are more prone to wind-induced vibration.
  • For portable Newtonians collimation can be a problem. The primary and secondary can get out of alignment from the shocks associated with transport and handling. This means the telescope may need to be re-aligned (collimated) every time it is set up. Other designs such as refractors and catadioptrics (specifically Maksutov cassegrains) have fixed collimation.
  • The focal plane is at an asymmetrical point and at the top of the optical tube assembly. For visual observing, most notably on equatorial mounts,[5] tube orientation can put the eyepiece in a very poor viewing position, and larger telescopes require ladders or support structures to access it.[6] Some designs provide mechanisms for rotating the eyepiece mount or the entire tube assembly to a better position. For research telescopes, counterbalancing very heavy instruments mounted at this focus has to be taken into consideration.

Variations

[edit]

There are several variations on the Newtonian design that add a lens to the system creating a catadioptric telescope. This is done to correct spherical aberration or reduce cost.

Schmidt–Newtonian

[edit]
Main article: Schmidt–Newtonian telescope
Schmidt–Newtonian telescope.

A Schmidt–Newtonian telescope combines the Newtonian optical design with a full-aperture Schmidt corrector plate in front of the primary mirror that not only corrects spherical aberration but can also support the secondary mirror. The resulting system has less coma and secondary mirror support induced diffraction effects.[7]

Maksutov–Newtonian

[edit]
Further information: Maksutov telescope

Similar to a Schmidt–Newtonian, a Maksutov telescope's meniscus shaped corrector can be added to the Newtonian configuration, which gives it minimal aberration over a wide field of view, with one-fourth the coma of a similar standard Newtonian and one-half the coma of a Schmidt-Newtonian.[8] Diffraction can also be minimized by using a high focal ratio with a proportionally small diagonal mirror mounted on the corrector.[9]

Jones–Bird

[edit]

A Jones–Bird Newtonian (sometimes called a Bird–Jones) uses a spherical primary mirror in place of a parabolic one, with spherical aberrations corrected by sub-aperture corrector lens[10] usually mounted inside the focusser tube or in front of the secondary mirror. This design reduces the size and cost of the telescope with a shorter overall telescope tube length (with the corrector extending the focal length in a "telephoto" type layout) combined with a less costly spherical mirror. Commercially produced versions of this design have been noted to be optically compromised, due to the difficulty of producing a correctly shaped sub-aperture corrector, and are targeted at the inexpensive end of the telescope market.[11]

History

[edit]
See also: History of the telescope

Newton's idea for a reflecting telescope was not new. Galileo Galilei and Giovanni Francesco Sagredo had discussed using a mirror as the image forming objective soon after the invention of the refracting telescope,[12] and others, such as Niccolò Zucchi, claimed to have experimented with the idea as far back as 1616.[13] Newton may even have read James Gregory's 1663 book Optica Promota which described reflecting telescope designs using parabolic mirrors[14] (a telescope Gregory had been trying unsuccessfully to build).[15]

Newton built his reflecting telescope because he suspected it could prove his theory that white light is composed of a spectrum of colours.[16] Colour distortion (chromatic aberration) was the primary fault of refracting telescopes of Newton's day, and there were many theories as to what caused it. During the mid-1660s with his work on the theory of colour, Newton concluded this defect was caused by the lens of the refracting telescope behaving the same as prisms he was experimenting with, breaking white light into a rainbow of colours around bright astronomical objects.[17][18] If this were true, then chromatic aberration could be eliminated by building a telescope which did not use a lens – a reflecting telescope.

A replica of a second reflecting telescope Newton presented to the Royal Society in 1672 (the first one he made in 1668 was loaned to an instrument maker but there is no further record of what happened to it).[19]

In late 1668 Isaac Newton built his first reflecting telescope. He chose an alloy (speculum metal) of tin and copper as the most suitable material for his objective mirror. He later devised means for shaping and grinding the mirror and may have been the first to use a pitch lap[20] to polish the optical surface. He chose a spherical shape for his mirror instead of a parabola to simplify construction; even though it would introduce spherical aberration, it would still correct chromatic aberration. He added to his reflector what is the hallmark of the design of a Newtonian telescope, a secondary diagonally mounted mirror near the primary mirror's focus to reflect the image at a 90° angle to an eyepiece mounted on the side of the telescope. This unique addition allowed the image to be viewed with minimal obstruction of the objective mirror. He also made the tube, mount, and fittings. Newton's first version had a primary mirror diameter of 1.3 inches (33 mm) and a focal ratio of f/5.[21] He found that the telescope worked without colour distortion and that he could see the four Galilean moons of Jupiter and the crescent phase of the planet Venus with it. Newton's friend Isaac Barrow showed a second telescope to a small group from the Royal Society of London at the end of 1671. They were so impressed with it that they demonstrated it to Charles II in January 1672. Newton was admitted as a fellow of the society in the same year.

Like Gregory before him, Newton found it hard to construct an effective reflector. It was difficult to grind the speculum metal to a regular curvature. The surface also tarnished rapidly; the consequent low reflectivity of the mirror and also its small size meant that the view through the telescope was very dim compared to contemporary refractors. Because of these difficulties in construction, the Newtonian reflecting telescope was initially not widely adopted. In 1721 John Hadley showed a much-improved model to the Royal Society.[22] Hadley had solved many of the problems of making a parabolic mirror. His Newtonian with a mirror diameter of 6 inches (150 mm) compared favourably with the large aerial refracting telescopes of the day.[23]

See also

[edit]

Notes

[edit]
  1. ^ Hall, A. Rupert (1992). Isaac Newton: Adventurer in Thought. Cambridge University Press. p. 67. ISBN 9780521566698.
  2. ^ Ingalls, Albert G., ed. (1935). Amateur Telescope Making (4th ed.). Munn and Co., Inc. [1]
  3. ^ Sacek, Vladimir (2006-07-14). "8.1.1. Newtonian off-axis aberrations". Retrieved 2009-09-29. off-axis performance of the paraboloidal mirror drops so quickly with the increase in relative aperture beyond ~ƒ/6
  4. ^ Knisely, David (2004). "Tele Vue Paracor Coma Corrector for Newtonians" (PDF). Cloudy Nights Telescope Review. Retrieved 2010-11-29.
  5. ^ Hebra, Alex (2010). The Physics of Metrology: All about Instruments: From Trundle Wheels to Atomic Clocks. Springer Science+Business Media. pp. 258–259. ISBN 978-3-211-78381-8.
  6. ^ Cooke, Antony (2009). Make Time for the Stars: Fitting Astronomy into Your Busy Life. Springer Science+Business Media. p. 14. ISBN 978-0-387-89341-9.
  7. ^ "Schmidt-Newton telescope". telescopeOptics.net. Retrieved 28 August 2012.
  8. ^ Rutten, Harrie G. J.; van Venrooij, Martin A.M. (1988). Telescope Optics: Evaluation and design. ISBN 9780943396187.
  9. ^ Mollise, Rod (28 February 2009). Choosing and Using a New CAT. p. 101. ISBN 9780387097725.
  10. ^ 10.1.2. Sub-aperture corrector examples: Single-mirror systems – Jones-Bird
  11. ^ "TELESCOPES – OVERVIEW AND TELESCOPE TYPES, CATADIOPTRIC NEWTONIAN". Archived from the original on 2020-08-11. Retrieved 2014-11-18.
  12. ^ Fred Watson (2007). Stargazer: The Life and Times of the Telescope. Allen & Unwin. p. 108. ISBN 978-1-74176-392-8.
  13. ^ The Galileo Project > Science > Zucchi, Niccolo
  14. ^ Derek Gjertsen (1986). The Newton Handbook. Routledge & Kegan Paul. p. 562. ISBN 978-0-7102-0279-6.
  15. ^ Michael White (1999). Isaac Newton: The Last Sorcerer. Basic Books. p. 169. ISBN 978-0-7382-0143-6.
  16. ^ Michael White (1999). Isaac Newton: The Last Sorcerer. Basic Books. p. 170. ISBN 978-0-7382-0143-6.
  17. ^ Newton thought little could be done to correct aberration short of making lenses that were f/50 or more."the object-glass of any telescope cannot collect all the rays which come from one point of an object, so as to make them convene at its focus in less room than in a circular space, whose diameter is the 50th part of the diameter of its aperture”
  18. ^ Stephen Parkinson (1870). A Treatise on Optics. Macmillan. p. 112.
  19. ^ Henry C. King (1955). The History of the Telescope. p. 74. ISBN 978-0-486-43265-6. Retrieved 2013-08-01.
  20. ^ Raymond N. Wilson (2007). Reflecting Telescope Optics I: Basic Design Theory and its Historical Development. Springer Science & Business Media. p. 9. ISBN 978-3-540-40106-3.
  21. ^ telescope-optics.net Reflecting Telescopes: Newtonian, two- and three-mirror systems
  22. ^ amazing-space.stsci.edu – Hadley’s Reflector
  23. ^ The complete Amateur Astronomer – John Hadley's Reflector

References

[edit]
Wikimedia Commons has media related to Newtonian telescopes.
  • Smith, Warren J., Modern Optical Engineering, McGraw-Hill Inc., 1966, p. 400
Retrieved from "https://en.wikipedia.org/w/index.php?title=Newtonian_telescope&oldid=1214400433"